111. Minimum Depth of Binary Tree

题目描述：

給定一個二元樹的根節點 root，找出其最小深度。最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。

葉子節點 是指沒有子節點的節點。

Example: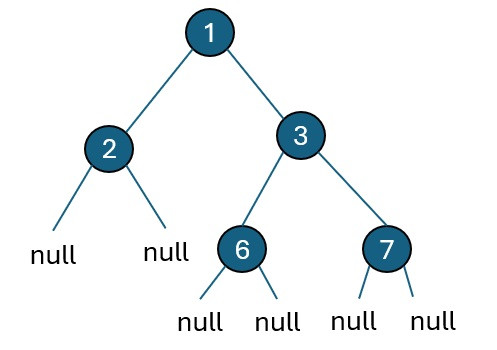

• Input: root = [1,2,3,null,null,6,7]
• Output: 2

解題思路:
這道題目是關於二元樹的實作題，有兩種常見的解法：遞迴法和迭代法。我們先介紹比較直觀的遞迴法來解決這個問題。

遞迴法的思路是通過遞歸地計算左子樹和右子樹的最小深度來找出二元樹的最小深度。具體步驟如下：

1. 檢查根節點是否為空：如果根節點為空，表示這棵樹沒有節點，直接返回深度為 0。

2. 處理子樹的情況：

   • 如果某一側子樹為空，則返回另一側子樹的最小深度加 1，因為此時最小深度只能來自非空的一側。
   • 如果兩側子樹都為空（表示當前節點是葉子節點），則按照前面的邏輯，會進入一側子樹為空的判斷，返回另一側的最小深度（即 0）加 1。
   • 如果兩側子樹都不為空，則比較兩者的最小深度，返回其中較小的深度加 1。

這樣的遞迴方法可以確保我們找到從根節點到最近葉子節點的最短路徑，從而計算出樹的最小深度。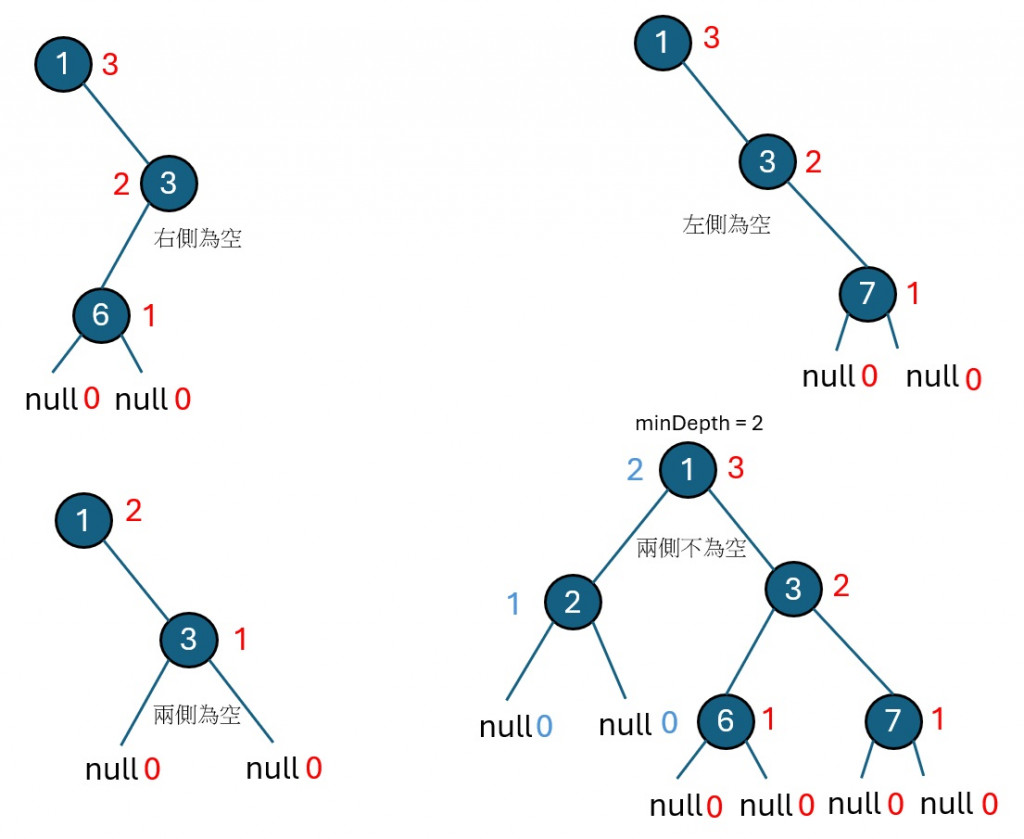

var minDepth = function(root) {
    if (!root) return 0;

    // If the left subtree is null, recursively find the min depth of the right subtree
    if (!root.left) return minDepth(root.right) + 1;

    // If the right subtree is null, recursively find the min depth of the left subtree
    if (!root.right) return minDepth(root.left) + 1;

    // If both subtrees are not null, return the minimum depth of the two subtrees plus one
    return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
};

時間複雜度：O(n)，其中 n 是二元樹中的節點數。每個節點都會被訪問一次。
空間複雜度：O(h)，其中 h 是二元樹的高度。遞迴call stack的深度取決於樹的高度。

迭代法的思路是通過廣度優先搜索（BFS） 來找出二元樹的最小深度。具體方法是從根節點開始逐層遍歷，每層遍歷時都將當前層的節點放入 queue 中。當遇到第一個葉子節點時，即沒有左或右子節點的節點，返回該葉子節點所在的深度。

由於廣度優先搜索採用的是先進先出（FIFO）的方式來處理節點，因此使用 queue 來實作是最佳選擇。在 queue 中，每次取出節點時，都會將該節點的左右子節點（如果有）加入 queue，直到找到第一個葉子節點為止。這樣的方法可以確保我們在最短路徑上找到最近的葉子節點，從而得出最小深度。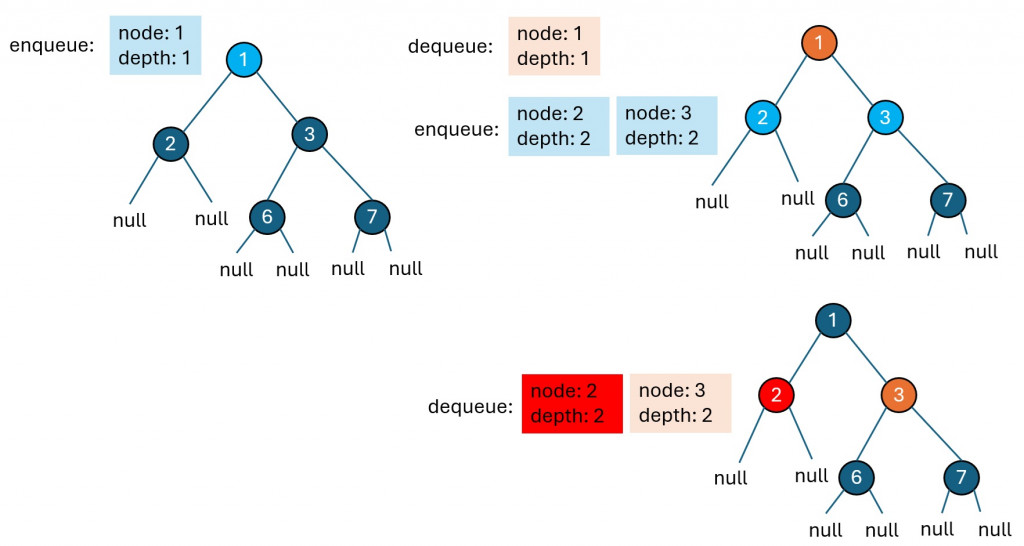

var minDepth = function(root) {
    if (root === null) return 0;

    let queue = [{ node: root, depth: 1 }];

    while (queue.length > 0) {
        let { node, depth } = queue.shift();

        if (node.left === null && node.right === null) {
            return depth;
        }

        if (node.left !== null) {
            queue.push({ node: node.left, depth: depth + 1 });
        }

        if (node.right !== null) {
            queue.push({ node: node.right, depth: depth + 1 });
        }
    }

    return 0;
};

時間複雜度：O(n)，其中 n 是二元樹中的節點數。每個節點都會被訪問一次。
空間複雜度：O(n)，在最壞情況下，queue中可能會包含所有節點。

總結:
這道題目可以歸類為「recursion」和「queue」這兩個分類。遞迴法直觀地利用樹的自然結構，簡單易學，特別適合初學者理解和學習樹的遍歷。然而，當處理左右子樹深度差異較大的情況時，遞迴深度可能會過深，導致較高的計算成本。

另一方面，迭代法（BFS）使用 queue 進行層序遍歷，能夠在最早發現葉子節點時就返回結果，通常比遞迴法更高效，特別是在樹不平衡的情況下。由於 BFS 可以更快地找到最近的葉子節點，因此在處理大規模或不平衡的樹時，迭代法更為實用。

這兩種方法各有優點，建議讀者根據具體情況選擇合適的解決方案。遞迴法適合用於學習和理解樹的基本概念，而迭代法則更常見於實際開發中。掌握這兩種方法，將有助於在不同場景下靈活應用。